Analysis of a Video of a Draughts Game using OpenCV and C++.

1. Pixel Classification

The first objective was to take a still image of the board and classify each of the pixels into one of five different categories: white squares, black squares, white pieces, black pieces or other. This can be accomplished using histogram back-projection, based on four sample images, each representing the colour of one of the first four pixel categories. This results in a grayscale probability image for each of the four pixel categories.

The final step is to move through every pixel in the original image one-by-one. The probability value for the given pixel in each of the four probability images is checked, and the image in which the probability (i.e. luminance value) is the highest is taken as the class to which that pixel belongs. To deal with the fifth possible category (other/background pixels) a probability threshold is used. If the highest probability that a pixel belongs to any of the four back-projected categories is below the threshold value, then the pixel is taken to be in the fifth category - in other words, if the probability that it belongs to any of the other four categories is too low, it is taken that it doesn't belong to any of them.

2. Identifying the Location of Each Piece

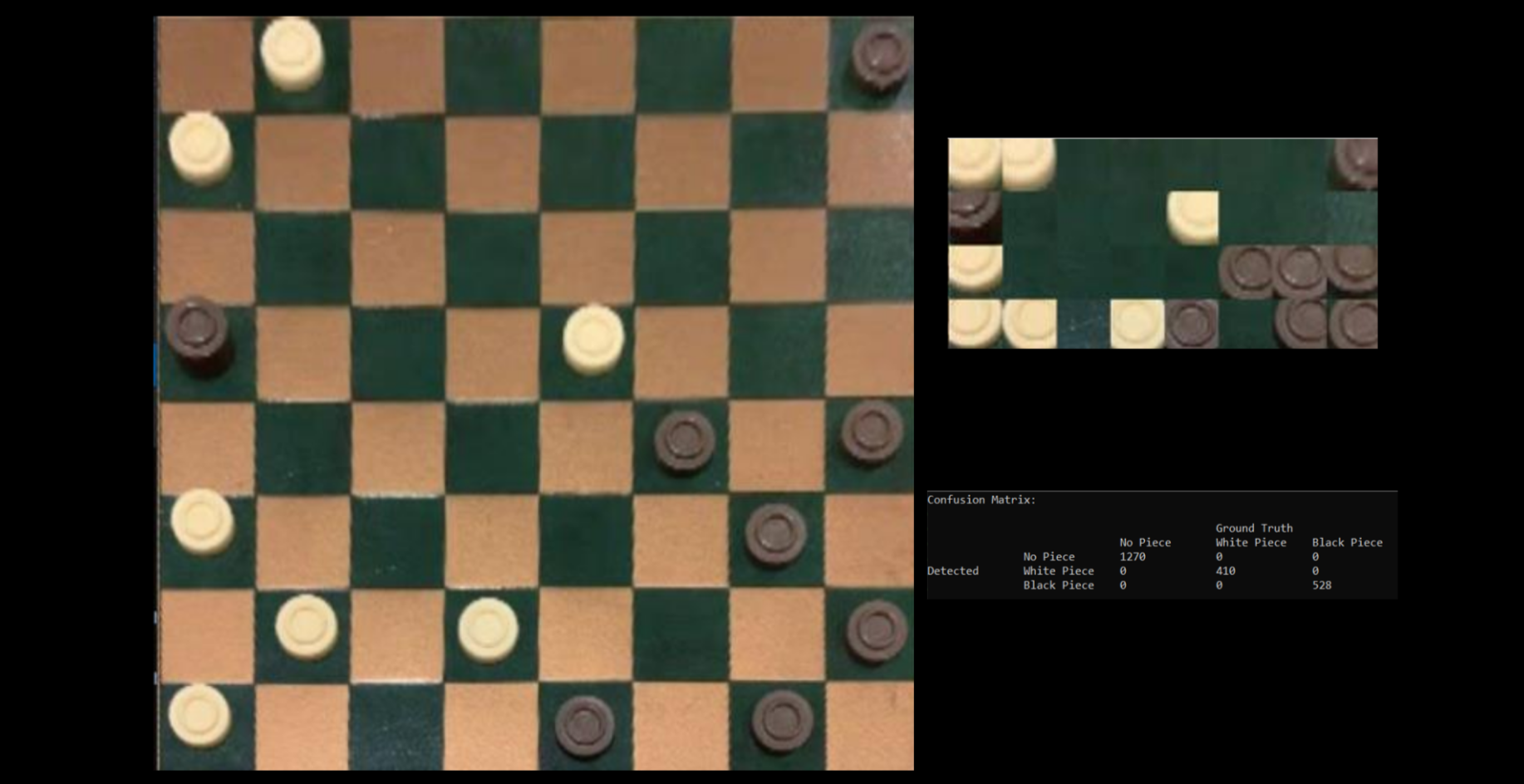
The next task involved determining if a piece was present in each square, and what type of piece - if any - was present. This could then be compared against a ground truth dataset for each of the still images.

Based on estimated values of the pixel locations for each of the four corners of the board, a perspective transformation can be performed, which in turn facilitates the segmentation of the board into individual squares. Assuming that pieces (if present) occupy the central portion of a square, the central subsection of each square is then isolated for analysis. Histograms for each of the three possible categories (empty black square, white piece, or black piece) are then generated, and the histogram of each square is compared against these using histogram correlation comparison. The category with the highest correlation is taken as the category of the square.

3. Extracting all Piece Moves that Occur in the Video

Next, the video of the draughts game was processed to identify the correct frames to process (a single still image for each board state) and to process and store the moves made during the game.

Still image extraction is achieved using the Gaussian Mixture Model. The method used to determine an appropriate time to take a screenshot is as follows: for every frame, the foreground image produced by the Gaussian Mixture Model is checked for non-zero value pixels. If the total number of non-zero pixels in the foreground is below a certain threshold value (determined by trial and error), this is taken as an indicator that a piece is not currently being moved. When this condition is met, a screenshot is taken. To avoid taking duplicate images of the same still image, a frame counter starts from zero after each screenshot, and the program will not attempt to take another screenshot until a threshold frame count value is exceeded.

After extracting the still frames, move detection is simple. First, the algorithm for piece locations developed in Part 2 is applied to each still frame. The moves made during the video are then found by simply comparing the piece locations for consecutive screenshots.

4. Using Edge Detection to Locate the Board Corners

While an estimate of the pixel locations of the board corners was used for the perspective transformation in Part 2, some experimentation was also performed with determining the exact location of each corner using edge detection. Several edge detection methods were investigated: Hough transformation for lines spanning the full image, probabilistic Hough transformation for line segments, contour segmentation, and finally the findChessboardCorners() OpenCV method.

5. Distinguishing between Normal Pieces and Kings using Hough Transform

Finally, code was developed to distinguish between normal pieces (men) and kings, and once again process the still images to produce an extended confusion matrix which considers white men, white kings, black men, black kings and empty squares as separate classes.

The work performed here is simply an extension of the algorithm outlined in Part 2. A perspective transformation is performed as in Part 2, then the resulting image is converted to grayscale before performing median filtering, which reduces the number of false circles detected by the Hough circle transform. A Hough transform is then performed on the smoothed grayscale image. The centre point of each resulting circle is used to determine which square it belongs to.

The result of these operations is an integer array that stores the number of circles detected in each square. The squares are then classified in the exact same way as in Part 2. Once each square has been classified as either empty, white or black, the circle number associated with each non-empty square is checked to determine if it contains a king or a regular piece.